Risk aversion
Risk aversion is a concept in psychology, economics, and finance, based on the behavior of humans (especially consumers and investors) while exposed to uncertainty.
Risk aversion is the reluctance of a person to accept a bargain with an uncertain payoff rather than another bargain with a more certain, but possibly lower, expected payoff. For example, a risk-averse investor might choose to put his or her money into a bank account with a low but guaranteed interest rate, rather than into a stock that may have high expected returns, but also involves a chance of losing value.
Outside the rather mathematical fields of economics and finance, people have to make choices about how they face risks every day. Some have become very cautious, preferring to minimize risks even when the potential benefit of an action is large.
Contents |
Example
A person is given the choice between two scenarios, one with a guaranteed payoff and one without. In the guaranteed scenario, the person receives $50. In the uncertain scenario, a coin is flipped to decide whether the person receives $100 or nothing. The expected payoff for both scenarios is $50, meaning that an individual who was insensitive to risk would not care whether they took the guaranteed payment or the gamble. However, individuals may have different risk attitudes. A person is said to be:
- risk-averse (or risk-avoiding) - if he or she would accept a certain payment (certainty equivalent) of less than $50 (for example, $40), rather than taking the gamble and possibly receiving nothing.
- risk-neutral - if he or she is indifferent between the bet and a certain $50 payment.
- risk-loving (or risk-seeking) - if the guaranteed payment must be more than $50 (for example, $60) to induce him or her to take the guaranteed option, rather than taking the gamble and possibly winning $100.
The average payoff of the gamble, known as its expected value, is $50. The dollar amount that the individual would accept instead of the bet is called the certainty equivalent, and the difference between the expected value and the certainty equivalent is called the risk premium. For risk-averse individuals, it becomes positive, for risk-neutral persons it is zero, and for risk-loving individuals their risk premium becomes negative.
Utility of money
In expected utility theory, an agent has a utility function u(x) where x represents the value that he might receive in money or goods (in the above example x could be 0 or 100).
Time does not come into this calculation, so inflation does not appear. (The utility function u(x) is defined only up to positive linear affine transformation - in other words a constant factor could be added to the value of u(x) for all x, and/or u(x) could be multiplied by a positive constant factor, without affecting the conclusions.) An agent possesses risk aversion if and only if the utility function is concave. For instance u(0) could be 0, u(100) might be 10, u(40) might be 5, and for comparison u(50) might be 6.
The expected utility of the above bet (with a 50% chance of receiving 100 and a 50% chance of receiving 0) is,
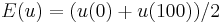 ,
,
and if the person has the utility function with u(0)=0, u(40)=5, and u(100)=10 then the expected utility of the bet equals 5, which is the same as the known utility of the amount 40. Hence the certainty equivalent is 40.
The risk premium is ($50 minus $40)=$10, or in proportional terms
or 25% (where $50 is the expected value of the risky bet: (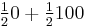 ). This risk premium means that the person would be willing to sacrifice as much as $10 in expected value in order to achieve perfect certainty about how much money will be received. In other words, the person would be indifferent between the bet and a guarantee of $40, and would prefer anything over $40 to the bet.
). This risk premium means that the person would be willing to sacrifice as much as $10 in expected value in order to achieve perfect certainty about how much money will be received. In other words, the person would be indifferent between the bet and a guarantee of $40, and would prefer anything over $40 to the bet.
In the case of a wealthier individual, the risk of losing $100 would be less significant, and for such small amounts his utility function would be likely to be almost linear, for instance if u(0) = 0 and u(100) = 10, then u(40) might be 4.0001 and u(50) might be 5.0001.
The utility function for perceived gains has two key properties: an upward slope, and concavity. (i) The upward slope implies that the person feels that more is better: a larger amount received yields greater utility, and for risky bets the person would prefer a bet which is first-order stochastically dominant over an alternative bet (that is, if the probability mass of the second bet is pushed to the right to form the first bet, then the first bet is preferred). (ii) The concavity of the utility function implies that the person is risk averse: a sure amount would always be preferred over a risky bet having the same expected value; moreover, for risky bets the person would prefer a bet which is a mean-preserving contraction of an alternative bet (that is, if some of the probability mass of the first bet is spread out without altering the mean to form the second bet, then the first bet is preferred).
The above is an introduction to the mathematics of risk aversion. However it assumes that the individual concerned will act entirely rationally and will not factor into his decision non-monetary, psychological considerations such as regret at having made the wrong decision. Often an individual may come to a different decision depending on how the proposition is presented, even though there may be no mathematical difference.
Measures of risk aversion
Absolute risk aversion
The higher the curvature of 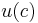 , the higher the risk aversion. However, since expected utility functions are not uniquely defined (are defined only up to affine transformations), a measure that stays constant with respect to these transformations is needed. One such measure is the Arrow-Pratt measure of absolute risk-aversion (ARA), after the economists Kenneth Arrow and John W. Pratt,[1][2] also known as the coefficient of absolute risk aversion, defined as
, the higher the risk aversion. However, since expected utility functions are not uniquely defined (are defined only up to affine transformations), a measure that stays constant with respect to these transformations is needed. One such measure is the Arrow-Pratt measure of absolute risk-aversion (ARA), after the economists Kenneth Arrow and John W. Pratt,[1][2] also known as the coefficient of absolute risk aversion, defined as
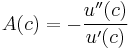 .
.
The following expressions relate to this term:
- Exponential utility of the form
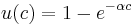 is unique in exhibiting constant absolute risk aversion (CARA):
is unique in exhibiting constant absolute risk aversion (CARA): 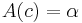 is constant with respect to c.
is constant with respect to c. - Hyperbolic absolute risk aversion (HARA) is the most general class of utility functions that are usually used in practice (specifically, CRRA (constant relative risk aversion, see below), CARA (constant absolute risk aversion), and quadratic utility all exhibit HARA and are often used because of their mathematical tractability). A utility function exhibits HARA if its absolute risk aversion is a hyperbolic function, namely
The solution to this differential equation (omitting additive and multiplicative constant terms, which do not affect the behavior implied by the utility function) is:
where 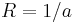 and
and 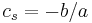 . Note that when
. Note that when 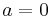 , this is CARA, as
, this is CARA, as 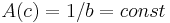 , and when
, and when 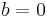 , this is CRRA (see below), as
, this is CRRA (see below), as 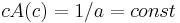 . See [3]
. See [3]
- Decreasing/increasing absolute risk aversion (DARA/IARA) is present if
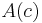 is decreasing/increasing. Using the above definition of ARA, the following inequality holds for DARA:
is decreasing/increasing. Using the above definition of ARA, the following inequality holds for DARA:
and this can hold only if 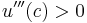 . Therefore, DARA implies that the utility function is positively skewed; that is,
. Therefore, DARA implies that the utility function is positively skewed; that is, 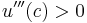 [4]. Analogously, IARA can be derived with the opposite directions of inequalities, which permits but does not require a negatively skewed utility function (
[4]. Analogously, IARA can be derived with the opposite directions of inequalities, which permits but does not require a negatively skewed utility function (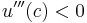 ). An example of a DARA utility function is
). An example of a DARA utility function is 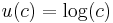 , with
, with 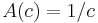 , while
, while 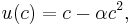
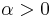 , with
, with 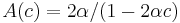 would represent a quadratic utility function exhibiting IARA.
would represent a quadratic utility function exhibiting IARA.
- Experimental and empirical evidence is mostly consistent with decreasing absolute risk aversion.[5]
- Contrary to what several empirical studies have assumed, wealth is not a good proxy for risk aversion when studying risk sharing in a principal-agent setting. Although
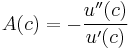 is monotonic in wealth under either DARA or IARA and constant in wealth under CARA, tests of contractual risk sharing relying on wealth as a proxy for absolute risk aversion are usually not identified.[6]
is monotonic in wealth under either DARA or IARA and constant in wealth under CARA, tests of contractual risk sharing relying on wealth as a proxy for absolute risk aversion are usually not identified.[6]
Relative risk aversion
The Arrow-Pratt measure of relative risk-aversion (RRA) or coefficient of relative risk aversion is defined as
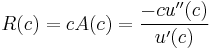 .
.
Like for absolute risk aversion, the corresponding terms constant relative risk aversion (CRRA) and decreasing/increasing relative risk aversion (DRRA/IRRA) are used. This measure has the advantage that it is still a valid measure of risk aversion, even if the utility function changes from risk-averse to risk-loving as c varies, i.e. utility is not strictly convex/concave over all c. A constant RRA implies a decreasing ARA, but the reverse is not always true. As a specific example, the expected utility function 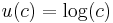 implies RRA = 1.
implies RRA = 1.
In intertemporal choice problems, the elasticity of intertemporal substitution is often unable to be disentangled from the coefficient of relative risk aversion. The isoelastic utility function
exhibits constant relative risk aversion with 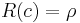 and the elasticity of intertemporal substitution
and the elasticity of intertemporal substitution 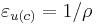 . When
. When 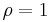 and one is subtracted in the numerator (facilitating the use of l'Hôpital's rule), this simplifies to the case of log utility, and the income effect and substitution effect on saving exactly offset.
and one is subtracted in the numerator (facilitating the use of l'Hôpital's rule), this simplifies to the case of log utility, and the income effect and substitution effect on saving exactly offset.
Implications of increasing/decreasing absolute and relative risk aversion
The most straightforward implications of increasing or decreasing absolute or relative risk aversion, and the ones that motivate a focus on these concepts, occur in the context of forming a portfolio with one risky asset and one risk-free asset.[1][2] If the person experiences an increase in wealth, he/she will choose to increase (or keep unchanged, or decrease) the number of dollars of the risky asset held in the portfolio if absolute risk aversion is decreasing (or constant, or increasing). Thus economists avoid using utility functions, such as the quadratic, which exhibit increasing absolute risk aversion, because they have an unrealistic behavioral implication.
Similarly, if the person experiences an increase in wealth, he/she will choose to increase (or keep unchanged, or decrease) the fraction of the portfolio held in the risky asset if relative risk aversion is decreasing (or constant, or increasing).
Portfolio theory
In modern portfolio theory, risk aversion is measured as the additional marginal reward an investor requires to accept additional risk. In modern portfolio theory, risk is being measured as standard deviation of the return on investment, i.e. the square root of its variance. In advanced portfolio theory, different kinds of risk are taken into consideration. They are being measured as the n-th radical of the n-th central moment. The symbol used for risk aversion is A or An.
Limitations
The notion of (constant) risk aversion has come under criticism from behavioral economics. According to Matthew Rabin of UC Berkeley, a consumer who,
from any initial wealth level [...] turns down gambles where he loses $100 or gains $110, each with 50% probability [...] will turn down 50-50 bets of losing $1,000 or gaining any sum of money.
It is noteworthy that Rabin's article went on to criticize the whole field of expected utility and not just constant relative risk aversion. This has led to some confusion in the field. One solution to the problem observed by Rabin is that proposed by prospect theory and cumulative prospect theory, where outcomes are considered relative to a reference point (usually the status quo), rather than to consider only the final wealth.
Risk aversion in the brain
Attitudes towards risk have attracted the interest of the field of neuroeconomics. A study by researchers at the University of Cambridge [7] suggested that the activity of a specific brain area (right inferior frontal gyrus) correlates with risk aversion, with more risk averse participants (i.e. those having higher risk premia) also having higher responses to safer options. This result coincides with other studies,[8][9] that show that neuromodulation of the same area results in participants making more or less risk averse choices, depending on whether the modulation increases or decreases the activity of the target area.
Public understanding and risk in social activities
In the real world, many government agencies, e.g. Health and Safety Executive, are fundamentally risk-averse in their mandate. This often means that they demand (with the power of legal enforcement) that risks be minimized, even at the cost of losing the utility of the risky activity. It is important to consider the opportunity cost when mitigating a risk; the cost of not taking the risky action. Writing laws focused on the risk without the balance of the utility may misrepresent society's goals. The public understanding of risk, which influences political decisions, is an area which has recently been recognised as deserving focus. David Spiegelhalter is the Winton Professor of the Public Understanding of Risk at Cambridge University; a role he describes as "outreach".[10]
A vaccine to protect children against the three common diseases measles, mumps and rubella was developed and recommended for all children in several countries including the UK. However, a controversy arose around allegations that it caused autism. This alleged causal link was thoroughly disproved,[11] and the doctor who made the claims was expelled from the General Medical Council. Even years after the claims were disproved, some parents wanted to avert the risk of causing autism in their own children. They chose to spend significant amounts of their own money on alternatives from private doctors. These alternatives carried their own risks which were not balanced fairly; most often that the children were not properly immunised against the more common diseases of measles, mumps and rubella.
Mobile phones may carry some small[12][13] health risk. While most people would accept that unproven risk to gain the benefit of improved communication, others remain so risk averse that they do not. (The COSMOS cohort study continues to study the actual risks of mobile phones.)
Risk aversion theory can be applied to many aspects of life and its challenges, for example:
- Bribery and corruption - whether the risk of being implicated or caught outweighs the potential personal or professional rewards
- Drugs - whether the risk of having a bad trip outweighs the benefits of possible transformative one; whether the risk of defying social bans is worth the experience of alteration. See "Harm reduction".
- Sex - judgement whether an experience that goes against social convention, ethical mores or common health prescriptions is worth the risk.
- Extreme sports - weighing the risk of physical injury or death against the adrenaline rush and bragging rights.
- Play by children in playgrounds or beyond the reach of their parents.
See also
- Ambiguity aversion
- Optimism bias
- Utility
- Risk premium
- Equity premium puzzle
- Investor profile
- Loss aversion
- St. Petersburg paradox
- Compulsive gambling, a contrary behavior
- Neuroeconomics
- Prudence in economics and finance
- Diminishing marginal utility
External links
- Paper about problems with risk aversion
- Economist article on monkey experiments showing behaviours resembling risk aversion (requires a paid subscription to economist.com)
- Arrow-Pratt Measure on About.com:Economics
- Risk Aversion of Individuals vs Risk Aversion of the Whole Economy
- The benefit of utilities: a plausible explanation for small risky parts in the portfolio
References
- ^ a b Arrow, K.J.,1965, "The theory of risk aversion," in Aspects of the Theory of Risk Bearing, by Yrjo Jahnssonin Saatio, Helsinki. Reprinted in: Essays in the Theory of Risk Bearing, Markham Publ. Co., Chicago, 1971, 90–109.
- ^ a b Pratt, J. W., "Risk aversion in the small and in the large," Econometrica 32, January–April 1964, 122–136.
- ^ Zender's lecture notes
- ^ Haim Levy (2006), Stochastic Dominance: Investment Decision Making under Uncertainty, Springer
- ^ Friend, Irwin and Blume, Marshall (1975), The Demand for Risky Assets, The American Economic Review.
- ^ Bellemare, Marc F. and Zachary S. Brown, On the (Mis)Use of Wealth as a Proxy for Risk Aversion[1], Working Paper, Duke University.
- ^ Christopoulos GI; Tobler PN; Bossaerts P; Dolan RJ; Schultz W (2009). "Neural Correlates of Value, Risk, and Risk Aversion Contributing to Decision Making under Risk.". J Neurosci 26 (24): 6469–6472. doi:10.1523/JNEUROSCI.0804-06.2006. PMID 16775134.
- ^ Knoch D, Gianotti LR, Pascual-Leone A, Treyer V, Regard M, Hohmann M, Brugger P (2006). "Disruption of right prefrontal cortex by low-frequency repetitive transcranial magnetic stimulation induces risk-taking behavior.". J Neurosci 26 (24): 6469–6472. doi:10.1523/JNEUROSCI.0804-06.2006. PMID 16775134.
- ^ Fecteau S, Pascual-Leone A, Zald DH, Liguori P, Théoret H, Boggio PS, Fregni F (2007). "Activation of prefrontal cortex by transcranial direct current stimulation reduces appetite for risk during ambiguous decision making.". J Neurosci 27 (23): 6212–6218. doi:10.1523/JNEUROSCI.0314-07.2007. PMID 17553993.
- ^ Spiegelhalter, David (Michaelmas 2009). "Don's Diary". CAM. 58. Cambridge University Alumni Association. p. 3. http://www.alumni.cam.ac.uk/uploads/File/CAM58/CAM58.pdf#page=5.
- ^ Madsen KM, Hviid A, Vestergaard M et al. (2002). "A population-based study of measles, mumps, and rubella vaccination and autism". N Engl J Med 347 (19): 1477–82. doi:10.1056/NEJMoa021134. PMID 12421889.
- ^ "What are the health risks associated with mobile phones and their base stations?". Online Q&A. World Health Organization. 2005-12-05. http://www.who.int/features/qa/30/en. Retrieved 2008-01-19.
- ^ "Electromagnetic fields and public health: mobile telephones and their base stations". Fact sheet N°193. World Health Organization. June 2000. http://www.who.int/mediacentre/factsheets/fs193/en. Retrieved 2008-01-19.
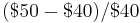
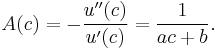
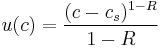
![\frac{\partial A(c)}{\partial c} = -\frac{u'(c)u'''(c) - [u''(c)]^2}{[u'(c)]^2} < 0](/2012-wikipedia_en_all_nopic_01_2012/I/6d5c1c14a9b520a79978cfb54b1ce7f9.png)
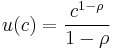
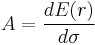
![A_n = \frac{dE(r)}{d\sqrt[n]{\mu_n}} = \frac{1}{n} \frac{dE(r)}{d\mu_n}](/2012-wikipedia_en_all_nopic_01_2012/I/bc4a948e9a3bb8e0ed8e54797f559679.png)